Mack's Stats

A. Based on Table 1 What is the probability of:

	B	B1
A	10	20
A1	20	40

A1. Event A:

P(A) = 30/90 = 0.33~
A2. Event B:

P(B) = 30/90 = 0.33~

A3. Event A or B (Not Mutually Exclusive):

(A U B) = P(A) + P(B) – P(A and B)

0.33 + 0.33 – (0.33*0.33) = 0.55

A4. P(A or B) = P(A) + P(B) (Mutually Exclusive):

P(A) + P(B) = 0.33 + 0.33 = 0.66

B. Applying Bayes’ Theorem 
Jane is getting married tomorrow, at an outdoor ceremony in the desert. In recent years, it has rained only 5 days each year. Unfortunately, the weatherman has predicted rain for tomorrow. When it actually rains, the weatherman correctly forecasts rain 90% of the time. When it doesn’t rain, he incorrectly forecasts rain 10% of the time.

What is the probability that it will rain on the day of Jane’s wedding? 

Solution: The sample space is defined by two mutually-exclusive events – it rains or it does not rain. Additionally, a third event occurs when the weatherman predicts rain. Notation for these events appears below.

Event A1. It rains on Jane’s wedding.
Event A2. It does not rain on Marie’s wedding.
Event B. The weatherman predicts rain.

In terms of probabilities, we know the following:
P( A1 ) = 5/365 =0.0136985 [It rains 5 days out of the year.]
P( A2 ) = 360/365 = 0.9863014 [It does not rain 360 days out of the year.]
P( B | A1 ) = 0.9 [When it rains, the weatherman predicts rain 90% of the time.]
P( B | A2 ) = 0.1 [When it does not rain, the weatherman predicts rain 10% of the time.]
We want to know P( A1 | B ), the probability it will rain on the day of Marie’s wedding, given a forecast for rain by the weatherman. The answer can be determined from Bayes’ theorem, as shown below.

P( A1 | B ) = P( A1 ) P( B | A1 )
P( A1 ) P( B | A1 ) + P( A2 ) P( B | A2 )
P( A1 | B ) = (0.014)(0.9) / [ (0.014)(0.9) + (0.986)(0.1) ]
P( A1 | B ) = 0.111
Note the somewhat unintuitive result. Even when the weatherman predicts rain, it only rains only about 11% of the time. Despite the weatherman’s gloomy prediction, there is a good chance that Marie will not get rained on at her wedding.
B1. Is this answer True or False.

This answer is true.
B2. Please explain why?

This answer can be proven with Baye’s Theorem

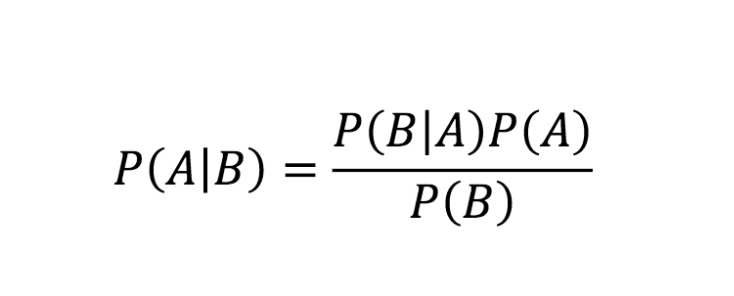
The scenario provided the values of A and P(B|A), so we were able to find P(A|B). Baye’s theory observes the relationship of conditional probabilities that are the reverse of each other. This is why it was easily applied to this situation.

C. Last assignment from our textbook, pp. 55 Exercise # 2.3.
For a disease known to have a postoperative complication frequency of 20%, a surgeon suggests a new procedure. She/he tests it on 10 patients and found there are not complications. What is the probability of operating on 10 patients successfully with the tradtional method?
A hint, use dbinom function – it is part of R functions that count Density, distribution function, quantile function, and random generation for the binomial distribution with parameters size and prob.

You will answer this question with
dbinom(XXX, size=XXX, prob=XXX)

I wanted to inspect this function more so I looked into its documentation.

Description
Density, distribution function, quantile function and random generation for the binomial distribution with parameters size and prob.

This is conventionally interpreted as the number of ‘successes’ in size trials.

Usage
dbinom(x, size, prob, log = FALSE)
pbinom(q, size, prob, lower.tail = TRUE, log.p = FALSE)
qbinom(p, size, prob, lower.tail = TRUE, log.p = FALSE)
rbinom(n, size, prob)
Arguments
x, q
vector of quantiles.

p
vector of probabilities.

n
number of observations. If length(n) > 1, the length is taken to be the number required.

size
number of trials (zero or more).

prob
probability of success on each trial.

log, log.p
logical; if TRUE, probabilities p are given as log(p).

lower.tail
logical; if TRUE (default), probabilities are P[X \le x]P[X≤x], otherwise, P[X > x]P[X>x].

With this in mind, I was able to execute the following code to solve the problem:

dbinom(0, size = 10, prob = 2/10)
[1] 0.1073742