Mack's Stats

From our textbook: pp. 188 Question 10.1 and 10.3

10.1
Set up an additive model for the ashina data, as part of ISwR package.

This data contain additive effects on subjects, period and treatment. Compare the results with those with those obtained from t tests. 

10.3. Consider the following definitions
a <- g1(2, 2, 8)
b <- g1(2, 4, 8)
x <– 1:8
y <- c(1:4, 8:5)
z <- rnorm (8)

Note:
The rnorm() is a built-in R function that generates a vector of normally distributed random numbers. The rnorm() method takes a sample size as input and generates that many random numbers.

Your assignment:
Generate the model matrices for models z ~ a*b, z ~ a:b, etc. In your blog posting discuss the implications. Carry out the model fits and notice which models contain singularities.
Hint
We are looking for:
model.matrix (~ a:b);   lm (z ~ a:b)

10.1

Step 1

In this first step I created data frames for the active and placebo groups.

Step 2

I then set up the additive model and fitted it.

Step 3

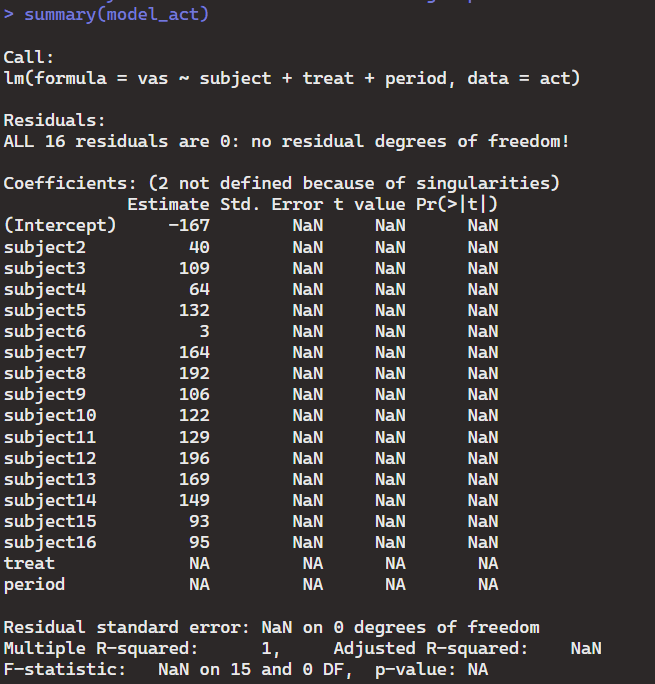
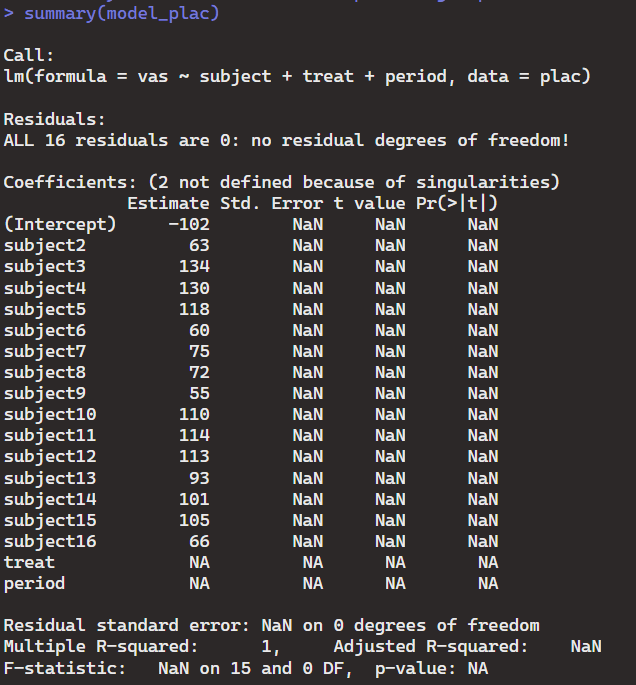
These summaries allow us to compare the two models.

Step 5

Finally, I set up the t.tests for comparison.

10.3

Step 1

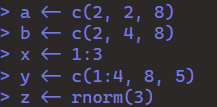
First I define my variables.

Step 2

Then I generate the models matrices and fit the models.

Step 3

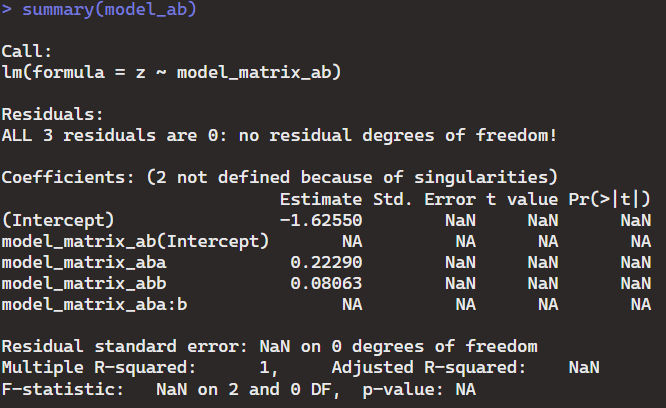
Implications:

1. Model z ~ a * b represents an interaction model where both ‘a’ and ‘b’ are considered as main effects, and their interaction term is included. This model allows for the examination of the combined effects of ‘a’ and ‘b’ on ‘z’.
2. Model z ~ a:b represents a model with an interaction term between ‘a’ and ‘b’. This model assesses the interaction effect between ‘a’ and ‘b’ on ‘z’ independently.

Singularities:
Singularities may occur when one or more variables in the model are linearly dependent, making it impossible to estimate the model parameters. In the context of these models, if ‘a’ and ‘b’ are highly correlated, or if their interaction perfectly predicts the response ‘z’, singularities may arise.

In this case, Model_ab has two singularitites and Model_a_colon_b has a singularity as well. This prevents R from producing some coefficients.