Mack's Stats

1. Setting up matrices A and B:

• I created two matrices, A and B, using the matrix() function in R.
• Matrix A contains numbers from 1 to 100, arranged in 10 rows and an unspecified number of columns (automatically calculated).
• Matrix B contains numbers from 1 to 1000, arranged in 10 rows and an unspecified number of columns (automatically calculated).

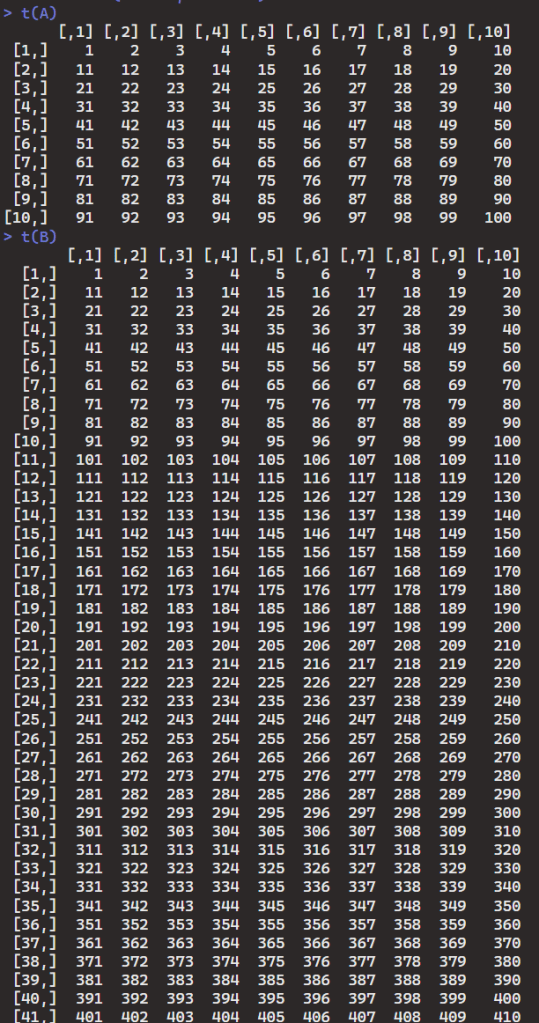
1. Transposing matrices A and B:

• Transposing a matrix involves flipping its rows and columns. I used the t() function in R to achieve this.
• The result of t(A) will be a matrix where the rows of A become the columns of the result, and vice versa. Similarly for matrix B.

• – 1000

1. Creating two vectors (a and b):

• I created two vectors, a and b, using the : operator to generate sequences of numbers.
• Vector a contains numbers from 1 to the number of columns in matrix A.
• Vector b contains numbers from 1 to the number of columns in matrix B.

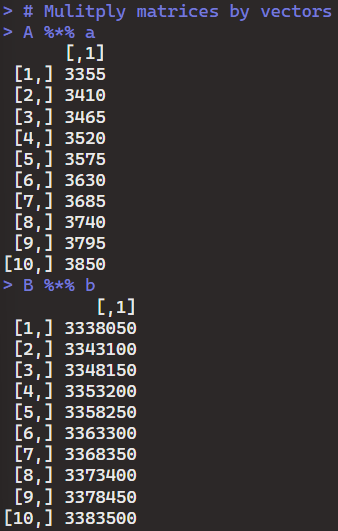
1. Multiplying matrices by vectors:

• I performed matrix-vector multiplication using the %*% operator.
• A %*% a will multiply matrix A by vector a.
• B %*% b will multiply matrix B by vector b.

1. Re-assigning the vectors a and b:

• I re-assigned vectors a and b to contain a sequence of 1s, with the length of the sequence being equal to the number of rows in matrices A and B, respectively.

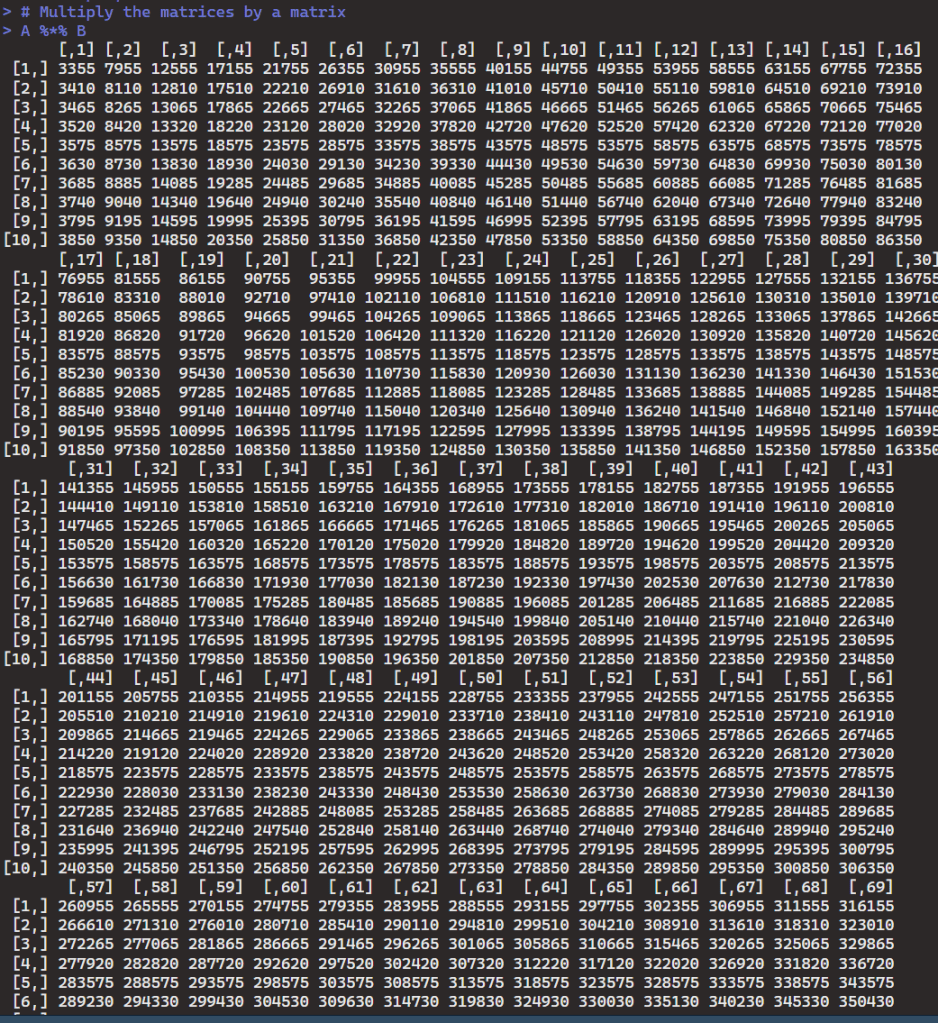
1. Multiplying the matrices by a matrix:

• I performed matrix-matrix multiplication using the %*% operator.
• A %*% B will multiply matrix A by matrix B. This operation is only valid if the number of columns in A matches the number of rows in B.

• etc.

1. Inversing matrix S and checking its determinant:

• Finally, I created a matrix S using the matrix() function, containing numbers from 2 to 5 arranged in 2 rows and 2 columns.
• I calculated the determinant of matrix S using the det() function. The determinant of a matrix is a scalar value that can be computed from its elements and is useful for various mathematical operations.

Link to Github Repository: https://github.com/mramalho4/rprog-repo.git